書名「算数で育てる学び合いのチカラ 〜つながる・深まる授業デザイン〜」（Amazon）

　

過去１０年以上前から現在までの算数学び合いで有効だった実践をまとめてみました。とりあえずAmazonでKindleの電子書籍として出していますが、紙書籍は後日出版する予定です。読んでいただければ幸いです。Amazon検索；「算数学び合い」、または「田井地清」

 

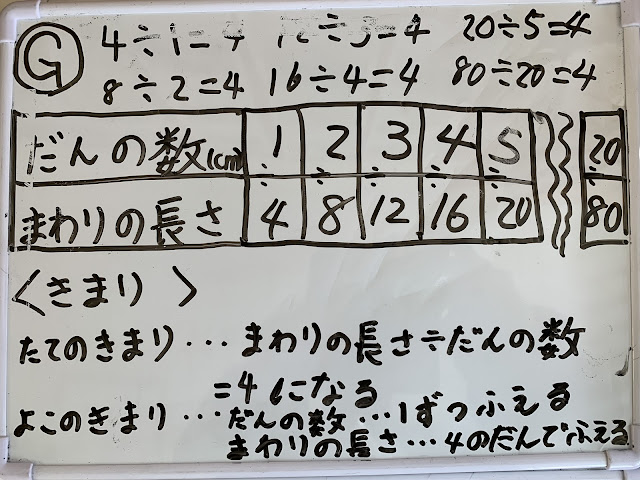
算数の予習で説明力UP!理解力UP!

 　

「面積」の学習から予習することを宿題にしています。予習カードを配布して、「わかったことは何か」と「わからないことは何か」を書いてくるように言いました。１日分の書くスペースは、そんなに広くないので、負担感はあまりないと思いますが、習っていないことをしっかり読まないと理解できないので、難しさはあります。

算数の授業では、いつもめあては「〜を説明しよう」という言葉を使っています。算数は、答えを求めれば終わりではなく、なぜそうなるのかを筋道立てて説明することで、論理的思考力が身に付くと考えています。ですから、今回の予習では、答えが何かではなく、どんな方法でどのように説明するかということを予習してくるわけです。

初めは、教科書に書いているまとめをそのまま写してくるだけの人が多かったのですが、やっているうちに少しずつ変化が見られました。まず、上の写真ですが、余りの１７について、「あまりの１７は、０．１が１７個分という意味だから１．７」というように、小数点をそろえる理由や説明をきちんと書けるようになってきた人が増えました。以前は何を書いたらよいかがわからないグループがあったのですが、今は予習をもとにして話し合う姿が見られるようになりました。さらに、予習カードだけでは足りないので、自主学習ノートに考えを書いてくる人もいます。

上の写真では、面積の予習で、「長方形の面積を求める時、１㎠が何個あるか数えてみたら、たてと横の長さをかけてみた答えと同じになったことが不思議だと思いました。」と書いてきました。こういう予習をしてくると、「なぜ」という意識で授業に臨むことができ、自分の解決できた喜びを味わうことにつながります。もちろん、理解にもつながります。

まだ今年から始めたばかりなので、学力にどうつながるのかなど十分に分析できていませんが、授業での意欲的な様子から、確実に効果は上がっていると思います。

学力テストに向けて

学力テストでよくある問題に取り組みました。

グループ学習を中心に話し合いました。

授業が終わってからも根気強く考えている子どもがいました。

 

小数のたし算を考える足場にした分数のたし算

 久しぶりの書き込みです。現在持ち上がりの４年担任をしています。

そこで、４年算数「分数」の実践です。

１０年前ぐらいまで、石田淳一教授による「考える足場」という指導法を実践していました。その後、学び合いの指導法に移行していましたが、久しぶりの「考える足場」です。

分数のたし算の学習では、テープ図などを用いて単位分数のいくつ分という考えをさせることが大事ですが、分数の問題提示の前に、０．２＋０．３＝０．５であることを説明させます。

０．１が何個分という整数に帰着させる見方、考え方ができるようにするためです。３年生の時の既習事項なので、比較的容易に説明することができます。

この考えをさせておくと、今回の分数のたし算の説明ができるようになります。しかも、グループ学習による学び合いで、一人一人が説明できるようになります。

最近は考える足場の授業を行なってきませんでしたが、この指導法は全員に容易に見通しを持たせることができます。この授業では、練習問題でも全員が説明できるようになりました。

数理的処理のよさを感じさせるには

お久しぶりです。今年度は、３年生の学級担任となり、また新たな気持ちで授業に取り組んでいます。ブログはちょっと間隔が空いてしまいましたが、日常の授業や学級経営に関わることをアップしていきたいと思います。

今年の冬に、２年生の算数の助言を頼まれ指導書を読んでいたら、「数理的な処理のよさ」という３０年？以上前からの言葉が目につきました。以前はよく聞く言葉でしたが、今の若い先生方は内容をわかっているのかなと思い、ブログにアップしてみようと思いました。

下の写真は、昨年度の４年生の授業のものです。授業では、「表を使ってきまりを見つけよう」という見通しにしたところ、ほとんどのグループで下の写真のように説明していました。

意図した通りの考えとなりました。しかし、本当にきまりを使うよさを感じることができたのだろうかと疑問に思いました。

そんな時、ある子どもがノートに一生懸命に図を描いていたのを発見しました。

「これは使える！」

と思い、さっそく写真を撮り電子黒板で提示しました。そしたら、「すごい！」という反応でした。何がすごいのかと問うと、

「めんどうくさいのによくやったなあ。」

という意味で「すごい」とのことでした。その後、拍手が起こりました。（というか、教師が価値づけによる拍手でした）

しかし、表と比較検討させると、きまりを使った方がはやくて簡単ということにまとまりました。ここで、なぜはやくて簡単ということを感じることができたかということです。それは、

「比べることでよさが浮き彫りになる」

ということなのです。一つの事例だけで、本当のよさは感じることは難しいと思います。そのことを伝えると、図で描いた人に改めて大きな拍手。この拍手は、よさを感じさせてくれたことに対する拍手です。

数理的処理のよさとはについてまとめてみました。

・数理的処理のよさとは？

子ども自らが日常の事象を算数の問題としてとらえ，既習の見方・考え方や知識・技

能を用いて数理的に処理していく際に，価値付けられる算数の特性のこと

まとめて言えば、

「簡潔・明瞭・一般」のこと

子どもたちには、「はかせどん」（はやい、かんたん、せいかく、どんなときもで

きる）と言っています。

•追体験（直接体験）

　よさを感じさせるには、追体験が有効です。練習問題として追体験させるのもア

リですが、追体験させた後に話し合いをさせることが大切。

•比較する

　よさは比較することによって浮き彫りになる。

•何と比べるのか

　既習の内容と比較 ・他者の考えと比較 ・困難な体験と比較 

今までの自分と比較 ・結果の比較（複数問題等への当てはめ）

•最後に、（ここ大事）

「よさは教えるものではなく、感じさせるもの」

 

分数も小数も整数も、すべて「単位のいくつ分」で説明させる

　４年算数「分数のたし算」

３、４年の分数指導をしていると、分数をたしてしまうという誤答が見受けられます。また、正答であっても、

「なんで分母は足さないの？」

と問うと、

「分子だけ足して分母は足してはいけないから。」

という子どもたちの反応が見られます。

分数指導で必ず心がけたいことは、「単位分数の何個分」という説明をさせることです。１０年以上前に、石田教授から教えていただいた「考える足場」を与えると、分母をたしてしまうという誤答がなくなり、その理由をしっかりと説明できるようになります。

そのために、低学年の

２００＋３００＝５００

という計算も、「１００のいくつ分」という考えで説明させることが大切です。

小数でも、

０．２＋０．３＝０．５の説明

まず、０．２は０．１が２個分

次に、０．３は０．１が３個分

だから、０．２＋０．３は０．１が（２＋３）個分で０．５

というように、単位小数０．１が何個分という説明をさせます。

３、４年の分数のたし算では、小数や整数のこの考え方を考える足場にして説明させます。小数を足場にして説明させると、分数でも分母を足すという誤答がなくなります。

これが高学年で分数のかけ算になっても、整数に帰着した考え方で説明できます。つまり、小学校の算数での十進法は、整数に帰着して指導していることを指導者がつかんでいることが大切です。

（以下、１１年前実践した考える足場の記事です）

https://vaio0819.blogspot.com/2011/02/blog-post_18.html

 

型を示す

 新学期が始まり１か月が過ぎました。今年度は４年生の担任ということでスタートしました。再任用２年目ですが、若者に負けないようにがんばります。

参観日の時に、「かさをつくろう」という小数のひき算の発展的な授業をしました。石田淳一教授の著書にあるものを自分なりにアレンジしてやってみました。

２つのコップを使ってかさをつくるという内容です。なみなみと入れた水を別のコップになみなみ入れると、元のコップに水が残る。つまり、ひき算した答えのかさだけ残るというものです。

これを論理的に表現させるというねらいです。説明の仕方はいろいろありますが、「まず」「次に」「だから」の型で表現させたいと考えました。でも、いきなりこの型で説明しなさいと言ってもなかなか難しいと思い、まず全体で学び合ってこの表現を完成させました。つまり、全体で解決したことを考える足場にするということです。

そしていよいよ主問題２をグループ学習させます。Ｔの文字にするので、「Ｔ字グループ」と呼んでいます。主問題1でやった表現を足場にしているので、どのグループも参考にしながら解いていました。

あるグループだけ、逆の発想をしていました。小さいコップから移す方法です。0.３Ｌなので、0.2Ｌと0.１Ｌでつくっていました。全体の話し合いで、0.１Ｌは半分まで水を入れるという説明でしたが、ちょうど半分というのは無理だということになりました。数学的には目盛りがないコップで半分という表現は、曖昧な言葉になります。

全体の話し合いのあとは、全員がこの表現で説明することができました。

今回の授業では、主問題1を全体で解決し、それを考える足場にして学び合うというものです。いろいろな表現をグループに出させて学び合うというやり方もありますが、論理的な説明をさせる場合は、型を示して教えなければなりません。時間ばかりかかり身につかない授業よりも、効率的で思考力、表現力が身につく授業だと思います。