新メンバー新たなスタート！「線対称な図形」

　新学年としてスタートして、早１か月が過ぎようとしています。新学年と言っても、学年の持ち上がり。ただ、人数減によりクラス替えがあり、３分の１のメンバーがかわりました。昨年度の５年生４クラスでは、グループ学習を積極的に取り入れていないクラスもあり、この研究会での「学び合い」の力には、差がありました。

　しかし、学び合いのやり方を示してやると、さすが６年生！すぐにやり方を覚えました。まずは、４，５月で、学び合いのスタイルを確立したいと思います。

さらに、今年度の校内研も、「学び合い」「考えをつなぐ」という言葉がキーワードになりそうですので、この研究会の趣旨にピッタリ当てはまります。

ところで、４月２３日は、対象図形の学習でした。人数が増え、９チーム編成でのチーム学習。ホワイトボードも２つ増やしての学び合い学習が始まりました。気付きでは、ほぼ全員の挙手ができるようになりました。相談タイムでは、相談後に必ず挙手するという約束のもと、２０秒間の話し合いをさせると、これも全員挙手ができました。今後の課題は、「考えをつなぐ」ということです。これができれば、あとは子供たち自ら学び合いができるようになり、教師はコーディネートしていけばよいことになります。

「線対称な図形の性質を見つけよう」というめあての下、気付きと見通しのあとのチーム学習です。最初の写真（チームE)では、対応する２点を結び直線は、対称の軸に垂直であることと、２等分する（軸までの長さが等しい）ことに気が付きました。（チームFも同様）数字が逆さまになっているのは、みんなで図形を取り囲んでいるからです。つまり、みんなでこの図を完成させているというわけです。
　

というわけで、線対称な図形の性質に気付くことができました。気付かなかったチームも、説明を聴いて理解できました。わからない子供に積極的に説明する子供の姿も見られ、まずはよいスタートとなりました。

ただ、チームの数が９に増え、各チームの考えをいかにしてコーディネートしていくかが課題となります。工夫としては、同じ考え同士をくっつけて黒板に貼ることで、事前に考え方別に仲間分けできるし、発表も効率的にできるということです。

また、石川県の神田先生から教えていただいたことですが、黒板の掲示した考えをじっくり見せて、気付いたことから発表させ、学び合うこということも有効であると思います。

いずれにせよ、学び合いを取り入れると子供たちが意欲的に学習し、学力が向上していきますが、チーム学習の時間の確保ということが課題となります。いかに効率的に学び合いを行うかが重要なカギとなります。

今後の成長が楽しみです！

意欲が高まり、学力が上がり、算数が好きになった子供たち

　５年担任としての１年が終了しました。この１年、算数の学び合いを自分なりに頑張っってきました。その成果として、学力が向上したのは、前のブログでも紹介しましたが、お楽しみ会の時に子供たちからいただいた寄せ書きを、家でじっくり読んでみました。

Ｃ１　算数の学び合いで平均点数が上がりました。

Ｃ２　苦手だった算数が楽しくなってきました。

Ｃ３　おかげで算数が楽しくなりました。

Ｃ４　私は、算数が苦手だったけど、おかげで分かりやすくてけっこういい点数がとれるようになりました。

Ｃ５　わかりやすく算数を教えてくださいました。とくに、算数に力を入れて教えてくださいました。学び合いも楽しかったです。

 

このように、１年間の思い出を中心とした寄せ書きに、算数の学び合いについて書いていた子供が何人もいました。

 

やはり、子供たち自身、学び合いのよさを実感していました。

 

さらに、２，３人の保護者の方から連絡帳でお礼のメッセージがありましたが、以下のような内容でした。

 

「○○は、去年まで算数が苦手でしたが、今年から算数がわかるようになって、好きになったようです。ありがとうございました。」

 

保護者の方々にも、子供が変わったことを実感していただきました。横国大の石田先生の著書に、「クラスが変わる、子供が変わる」という表現がありましたが、まったくその通りです。他のクラスの担任も、「子供がどんどん変わってきた！」と話していました。

 

単なる「伝え合い」から「学び合い」への転換が、今後の研究の中心になっていくと思いました。

 

 

 

 

学び合いで学力アップ実証

 

卒業式も終わり、学年末事務真っ最中。子供たちは春休みですが、まだまだ仕事が続きます。

仕事の合間に、先日の学力テスト（ＮＲＴ）の結果を、部分的ですが分析してみました。

全学年の算数の平均より４ポイントほど上がりました。ＣＲＴですが、前の学校でも、学び合いをしていないクラスと平均が１０ポイント以上上だったということを思い出しました。

うちの学校で、他にも学び合いを中心として指導してきた学級がありましたので、どんなものなのか分析をしていただきました。やはりどちらも４ポイントほど上がっていました。

学力を向上させたのは、学び合いによるものかどうかは、もう少し詳しく分析する必要がありますが、学び合いを中心とした授業改善により、確実に学力を向上させるということを実感しています。どうして向上するのかは、次のブログにてアップしてみたいと思います。

横浜国立大学の石田先生によれば、学び合いは確実に学力をアップさせることができるとおっしゃっています。今年も、そのことを実証できました。

 

反転授業の可能性と課題

期末事務も山場を越えました。そろそろ春の足音が聞こえてくる季節です。春が待ち遠しいですね。


さて、本日（３月１２日）のニュース２３を見ていたら、佐賀の自治体で全小学校が『反転授業』を導入しているというニュースが出ていました。

今までの算数学習で、当たり前とされてきた、「課題解決の授業」⇒「復習」
というスタイルから、『予習』⇒『学び合いの授業』
という、いわゆる反転授業を自治体ずべての小学校で行っているということです。自治体すべてというのが全国初ということです。

全国から教員が授業や講演に足を運んでいて、話題になっているとのこと。

予習に必要なのは、まずはタブレット。（これは金がかかる）ということで、自治体がかなりの予算を投入しているそうです。

予習をした子供たちは、翌日の授業で、話し合いを中心とした授業になるということです。

予習のデータとなる教材開発は、塾などの企業と現場の教員で作り上げているそうです。個人的にやるには、パソコンの知識や技術が必要だし、タブレットという高額なものを一人一人に準備するだけの予算が必要ですね。

最後に、課題としてまとめていました。

　

 

 ニュースの最後に、反転授業の課題として、いくつか挙げていました。

 

「議論をまとめる教師の技量」について

　これは、現在も全国の小学校算数授業の課題です。でも、今までと違うのは、予習を前提とした授業での話し合いをいかに練り上げるかということですね。議論をまとめることについては、先日、東京で行われた新算研での討論会で一番の話題として取り上げられました。この討論会の記事が東洋館出版の「新しい算数研究」（５月号）に特集として掲載されますので、ご覧下さい。

 

「動画を作る教師の負担」について

　まずは、それを作るソフトであるとか知識や技量が必要になり、予習教材にかかり時間は、かなりかかりそうです。しかも、ほとんどの授業分作ることになることから、かなりの負担増です。しかし、佐賀の自治体のように協同で取り組めば、比較的容易になるということでしょう。

 

「家庭や地域による格差」について

やはりタブレットは高額なので、自治体が賛同しなければ予算化できません。ＩＣＴのスクプレなどもそうですが、予算化については時間がかかりそうです。

 

もう一つ課題となるのが、現場の教師全員が賛同してくれるかということです。特にベテランの先生方は、過去の素晴らしい実践をたくさん持っています。今回のような、新しい授業を取り入れる時は、佐賀の例のように、みんなでやるという組織的な動きがあった方が、成果として出しやすいかもしれません。

 

このニュースを見てすぐにに思ったことは、今我々が取り組んでいる「学び合い」の考え方とかなり共通点があるということです。授業では、学び合いが中心となるという点です。

 

数か月前、朝日新聞にこれ（タブレットを使った反転授業）と同じ実践が掲載されていました。今回の注目すべき点は、自治体の小学校全てで行っているということです。

 

しかし、莫大な予算が必要なことですので、自治体の理解を得るのは大変なことです。佐賀の取り組みで、学力テストの数値が飛躍的にアップすれば、確実に広がっていくはずです。

 

とりあえず、学び合いはもちろん、予習のさせ方について検討していきたいと考えています。

 

ちなみに、東洋館出版の「新しい算数の授業」の来年度のテーマは、「学び合い」だそうです。

 

 

 

 

 

 

東京書籍Eネット掲載

関東甲信にかけて、大雪ですね。米沢は毎年豪雪なので、普通に生活してます(^^)

東京書籍Eネットに実践がアップされました。学び合いのよさを中心にまとめてみました。〔学び合い〕で検索してみて下さい。

https://ten.tokyo-shoseki.co.jp/material/new2/

ゆとり世代は習ってない台形の求積と公式

本日は、はるばる愛知県の小学校からＡ先生がお出でになりました。石田先生からのご紹介ということでした。二夜に渡って、おもてなしをさせていただきました。

さて、台形の求積と公式化の授業です。面積の数時間目なので、既習の図形に直すことを自然に考えられるようになっていました。「移動法」と名付けた等積変形や「倍割法」と名付けた倍積変形など、容易に見通せるようになりました。習っていないことでも、既習を使えば解けるという感覚が、少しずつ身に付いてきました。

グループ学習では、見通しで出ていない方法も、いろいろと出されました。
１　同じ台形をくっつけて平行四辺形にする方法
２　対角線で２つの三角形に分けてそれぞれの面積を求め、合わせる方法。

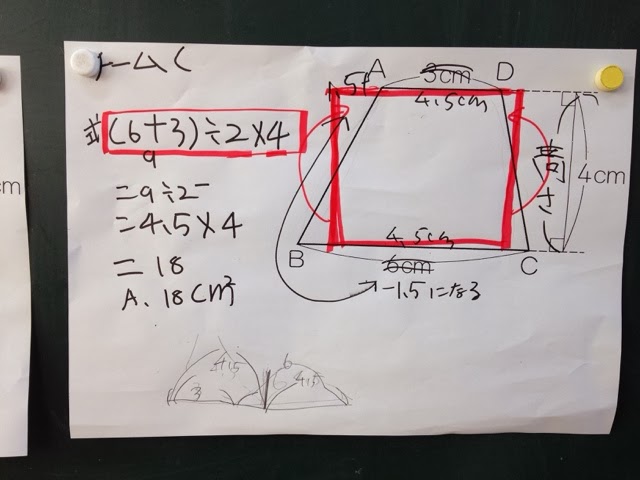
ここまでは、見通しで出されたものでした。見通しの時、Ａ君から「下の辺の長さと、上の辺の長さを同じにして求めます。」という意見が出されました。他の子供たちは、同じにするということが理解できずにいました。（３＋６）÷２＝４．５だからという説明でしたが、図のイメージが持てないので、グループ学習で説明を考えてもらうことにしました。

＜平行四辺形にする方法。＞

＜平行四辺形と三角形に分ける方法＞

＜つけたして平行四辺形にし、たしｔ三角形を引く方法＞

＜両端の出ている直角三角形を切って、上方のにつけて長方形に直す方法＞

 

この方法では、やはりみんなが理解できなかったので、赤のマジックで示してあげました。公式にも直結するので、この発想を大事にしたいと思い、取り上げました。

 

どの方法からも、公式化ができますが、まずは平行四辺形に直す方法が、公式化につながるので、上底、下底、高さという言葉を確認してから、公式化を図りました。チームＣでは、÷２と×４が逆になっているだけで、同じであることを確認しました。

 

ゆとり教育では、台形の面積の公式化はなかったのですが、やはりこの授業をするとわかりますが、どんな四角形でも求積できた方が、考える力がつくし楽しいですよね。

 

 

 

 

 

 

三角形から取り扱うよさは？

 

５年算数「面積」

 

「三角形の面積から平行四辺形の面積に入る指導のよさは何だろう。」と思いながら平行四辺形の求積に入りました。

 

１つ目の方法は、予想通り、直角三角形を移動する、等積変形「移動法」をするという考え方です。

 

２つ目は、１人の男子が思いついた、任意の高さで切って移動する方法です。

 

１と２は、容易に思いつくだろうと思っていました。

 

さて、３つ目の考え方です。既習の三角形が２つ分あるので、底辺×高さ÷２×２という説明でした。この方法は、教科書にも載っているので、子供たちから出なかった紹介しようと思っていた方法です。思いついた子供の説明を聞いてみると、

 

「昨日、どんな四角形でも、対角線で２つの三角形に分けることができると習ったので、平行四辺形もできると思い、分けてみました。そしたら、同じ三角形が２つ分になっているので、三角形の面積を２倍すれば求められます。」

 

　

その子供の説明を聞いて、なるほどと思ったことがあります。

 

その１；既習事項をしっかり想起して、問題解決していること。

その２；多角形の基本は三角形であるという、平面図形の特徴を理解することで、どんな多角形でも三角形に分ければ求められるということがわかる。

 

その２については、このように数学的な考え方を養うことだけでなく、今後、台形やひし形の求積で対角線を引き三角形に直して考えるという学習をします。

 

平行四辺形を先に扱い、三角形は平行四辺形の半分という考えやすさを求めるか、数学的な見方考え方を養うことで台形などへの拡張性を狙うかは、指導者の考えによるものであるが、教科書を鵜呑みにせず、どういう単元の展開にするか、さらにはどんな力を子供につけたいのかをじっくりと考えるべきですね。