三角形が先か、平行四辺形が先か！（５年「面積」より）

遅れましが、今年もよろしくお願いいたします。

さて、５年３学期は「面積」の単元からです。
５年の面積では、平行四辺形と三角形のどちらを先に扱うかで、指導の流れが変わりますが、使用している教科書では、平行四辺形の後に三角形を扱っています。

平行四辺形を先に扱うよさは、三角形は平行四辺形を２で割ればよいということも、解法の一つとして取り上げることができ、計算が単純化できることにあると思います。

三角形から入るよさは、多角形の基本は三角形であることや、三角形をもとにして考えると四角形に発展できるという数学的な考えを教えられることにあると思います。

今回は、多角形の基本である三角形をきちんと吟味することで、多角形に拡張できるというよさを実感させるために、三角形から入りました。

１教時目は、直角三角形の求積でした。この時間に、倍積変形と等積変形について学習しました。さらに、「倍割法」、「移動法」というネーミングにしました。

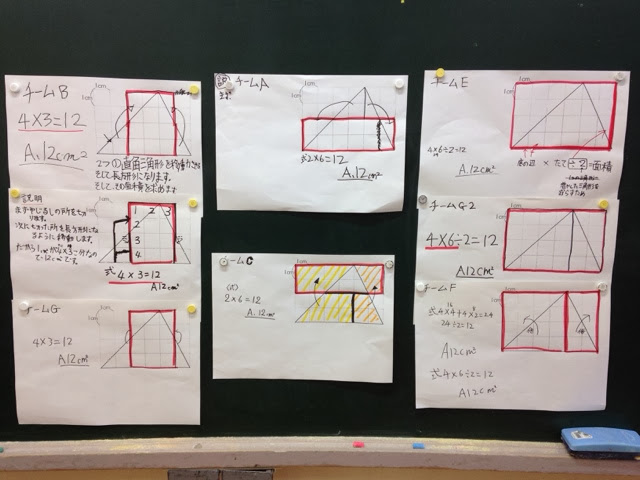
直角三角形でやった２つの方法を使えば、容易に求積せきるという見通しを持たせ、グループの話し合いに入りました。（下写真）

 

各チームごとに、いろいろな説明がありましたが、基本は「移動法」と「倍割法」でした。この中で、チームＣが台形を移動していたことに、驚かされました。

「子供の発想って、おもしろいなあ」と、感心してしまいました。

 

さて、これを次時で公式化するわけです。「底辺×高さ÷２」という公式を知っている子供もいますが、やはりなぜその公式なのかを、十分に時間をかけて考えさせることが大切だと思います。そうすることにより、多角形の求積への興味関心も高まり、いろいろな見方ができるようになるでしょう。

 

三角形か平行四辺形かについては、いろいろな情報をいただきたいと思っております。