ゆとり世代は習ってない台形の求積と公式

本日は、はるばる愛知県の小学校からＡ先生がお出でになりました。石田先生からのご紹介ということでした。二夜に渡って、おもてなしをさせていただきました。

さて、台形の求積と公式化の授業です。面積の数時間目なので、既習の図形に直すことを自然に考えられるようになっていました。「移動法」と名付けた等積変形や「倍割法」と名付けた倍積変形など、容易に見通せるようになりました。習っていないことでも、既習を使えば解けるという感覚が、少しずつ身に付いてきました。

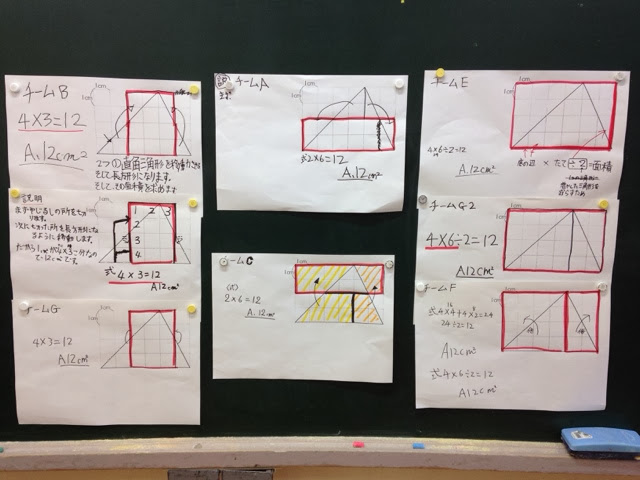
グループ学習では、見通しで出ていない方法も、いろいろと出されました。
１　同じ台形をくっつけて平行四辺形にする方法
２　対角線で２つの三角形に分けてそれぞれの面積を求め、合わせる方法。

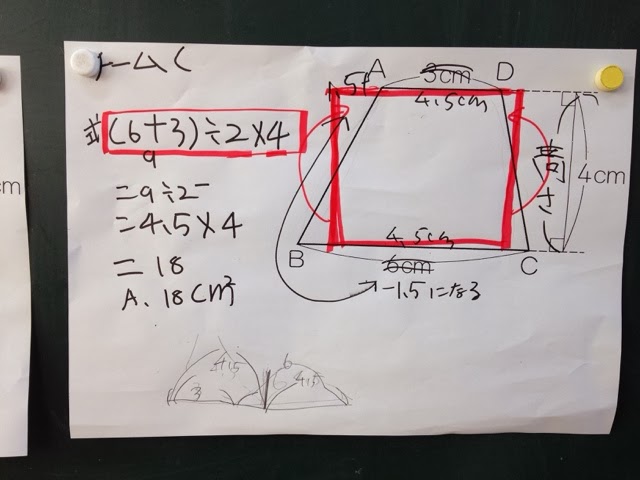
ここまでは、見通しで出されたものでした。見通しの時、Ａ君から「下の辺の長さと、上の辺の長さを同じにして求めます。」という意見が出されました。他の子供たちは、同じにするということが理解できずにいました。（３＋６）÷２＝４．５だからという説明でしたが、図のイメージが持てないので、グループ学習で説明を考えてもらうことにしました。

＜平行四辺形にする方法。＞

＜平行四辺形と三角形に分ける方法＞

＜つけたして平行四辺形にし、たしｔ三角形を引く方法＞

＜両端の出ている直角三角形を切って、上方のにつけて長方形に直す方法＞

 

この方法では、やはりみんなが理解できなかったので、赤のマジックで示してあげました。公式にも直結するので、この発想を大事にしたいと思い、取り上げました。

 

どの方法からも、公式化ができますが、まずは平行四辺形に直す方法が、公式化につながるので、上底、下底、高さという言葉を確認してから、公式化を図りました。チームＣでは、÷２と×４が逆になっているだけで、同じであることを確認しました。

 

ゆとり教育では、台形の面積の公式化はなかったのですが、やはりこの授業をするとわかりますが、どんな四角形でも求積できた方が、考える力がつくし楽しいですよね。

 

 

 

 

 

 

三角形から取り扱うよさは？

 

５年算数「面積」

 

「三角形の面積から平行四辺形の面積に入る指導のよさは何だろう。」と思いながら平行四辺形の求積に入りました。

 

１つ目の方法は、予想通り、直角三角形を移動する、等積変形「移動法」をするという考え方です。

 

２つ目は、１人の男子が思いついた、任意の高さで切って移動する方法です。

 

１と２は、容易に思いつくだろうと思っていました。

 

さて、３つ目の考え方です。既習の三角形が２つ分あるので、底辺×高さ÷２×２という説明でした。この方法は、教科書にも載っているので、子供たちから出なかった紹介しようと思っていた方法です。思いついた子供の説明を聞いてみると、

 

「昨日、どんな四角形でも、対角線で２つの三角形に分けることができると習ったので、平行四辺形もできると思い、分けてみました。そしたら、同じ三角形が２つ分になっているので、三角形の面積を２倍すれば求められます。」

 

　

その子供の説明を聞いて、なるほどと思ったことがあります。

 

その１；既習事項をしっかり想起して、問題解決していること。

その２；多角形の基本は三角形であるという、平面図形の特徴を理解することで、どんな多角形でも三角形に分ければ求められるということがわかる。

 

その２については、このように数学的な考え方を養うことだけでなく、今後、台形やひし形の求積で対角線を引き三角形に直して考えるという学習をします。

 

平行四辺形を先に扱い、三角形は平行四辺形の半分という考えやすさを求めるか、数学的な見方考え方を養うことで台形などへの拡張性を狙うかは、指導者の考えによるものであるが、教科書を鵜呑みにせず、どういう単元の展開にするか、さらにはどんな力を子供につけたいのかをじっくりと考えるべきですね。

三角形が先か、平行四辺形が先か！（５年「面積」より）

遅れましが、今年もよろしくお願いいたします。

さて、５年３学期は「面積」の単元からです。
５年の面積では、平行四辺形と三角形のどちらを先に扱うかで、指導の流れが変わりますが、使用している教科書では、平行四辺形の後に三角形を扱っています。

平行四辺形を先に扱うよさは、三角形は平行四辺形を２で割ればよいということも、解法の一つとして取り上げることができ、計算が単純化できることにあると思います。

三角形から入るよさは、多角形の基本は三角形であることや、三角形をもとにして考えると四角形に発展できるという数学的な考えを教えられることにあると思います。

今回は、多角形の基本である三角形をきちんと吟味することで、多角形に拡張できるというよさを実感させるために、三角形から入りました。

１教時目は、直角三角形の求積でした。この時間に、倍積変形と等積変形について学習しました。さらに、「倍割法」、「移動法」というネーミングにしました。

直角三角形でやった２つの方法を使えば、容易に求積せきるという見通しを持たせ、グループの話し合いに入りました。（下写真）

 

各チームごとに、いろいろな説明がありましたが、基本は「移動法」と「倍割法」でした。この中で、チームＣが台形を移動していたことに、驚かされました。

「子供の発想って、おもしろいなあ」と、感心してしまいました。

 

さて、これを次時で公式化するわけです。「底辺×高さ÷２」という公式を知っている子供もいますが、やはりなぜその公式なのかを、十分に時間をかけて考えさせることが大切だと思います。そうすることにより、多角形の求積への興味関心も高まり、いろいろな見方ができるようになるでしょう。

 

三角形か平行四辺形かについては、いろいろな情報をいただきたいと思っております。