前時の誤答を次の意欲にするためのコツ

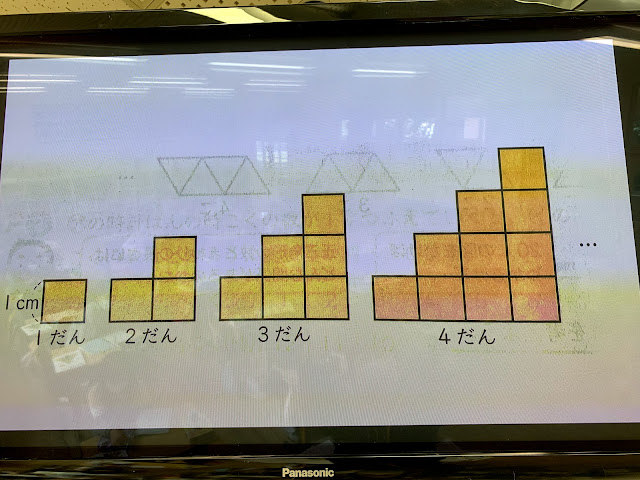
階段式の正方形が並ぶ図形。正方形の数とまわりの長さとのきまりを見つけて解く問題です。

前時で、時計の問題を話し合っていた時、縦の見方と横の見方が出されていました。２つとも、比例関係を前提とした考えが出されていましたが、それは比例関係ではないので、２つの考えは間違いということになりました。

しかし、縦・横に何倍になっているかをいう見方は、とても重要であることを教え、その考えをしたグループに大きな拍手をしていました。それは、次の時間や高学年の比例の時に大事な見方になるからです。

＜板書＞

前時に縦の見方で、何倍という決まった数を見つけて解いたグループが５つありました。

案の定、前時で横の倍関係を見つけた人がいたグループでは、横に何倍になっているかという関係性を見いだしていました。それを覚えていたせいか、他のグループも影響されて横の見方をしていました。

前時の誤答が本時に活かされたという授業になりました。

上のノートは、ある男の子が学び合いの時にじっくりと書いていたものです。この子は、普段はそんなに熱心に書いたりしないのですが、算数日記を褒められたりして意欲が高まったのでしょう。

前時で誤答だった２つのグループも、とてもよい考えだということを全体の前でほめて価値づけたことで、本時の意欲につながりました。他のグループもそれに感化されて今日の授業につながりました。

子どもって、こんなふうに変わっていくのですね。

そして、せっかく白熱した学び合いになったので、ホワイトボードを廊下に掲示しました。

先生方や他学年の人からの反響があればいいですね。